DANG Project - Descriptive, Algebraic, Numeric, and Graphic
Relating functions and their derivatives using various representations.
-
Purpose: The following pages are to be used as a matching game for individual advanced (calculus) math students or small groups of students to become familiar with the various representations of specific functions.
-
Explanation: Each page has the same 12 functions represented in 6 different ways: functional values, functional notation, graph, english description, the graph of the derivative (or slope), and the english description of the derivative (or slope). The student is to match each specific function across the 6 different representation. In other words, one function will be represented by a group (or row) consisting of 6 separate small boxes (or labels).
-
Preparation: for each page, the teacher should print out and hand to student(s) as described below:
- Page A (Student Answer Sheet / Analysis Questions) should be printed and handed out to students prior to the remaining sheets so that the students will be considering their answers as they complete the matching game
- Page 0 - Could be printed and handed to students. Page 0 contains the cordinate values -- x, f(x) --of the 12 function at various coordinates. Because providing this page may simplify some of the matching considerably, teachers may omit this page and the remaining sheets will still provide matching functions. Students should be aware of the number of digits given and rounding considerations. Values given as integers are not exact (as noted by the decimal point on the coordinates).
- Page 1 - Page 5 (representations of 12 functions) should be printed on separate sheets of paper and handed to each student (or group).
- Page 4 & 5 - may be omitted for non-Calculus students.
- Alternatively, the teacher may print each of the sheets on different colored paper and each box/label (12 per page) could be cut out and laminated before handing out to students.
- Key - answers to the matching game are to be given to students after they have completed their Page A - Student Answer sheet to be scored.
-
Page A - Student Answer / Analysis Questions Sheet
-
Page 0 - Function Values, labeled V1-V12 [be careful of the number of digits given and rounding considerations]
-
Page 1 - Function Notation, labeled E1-E12
-
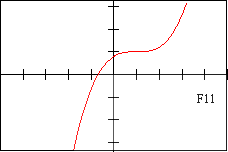
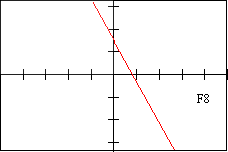
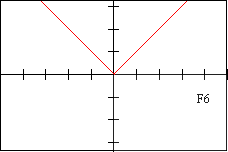
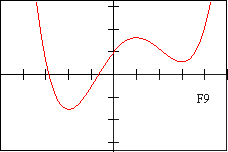
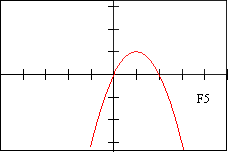
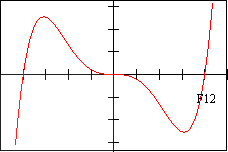
Page 2 - Function Graphs, labeled F1-F12
-
Page 3 - Function Descriptions, labeled f1-f12
-
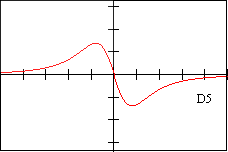
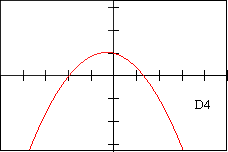
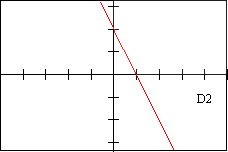
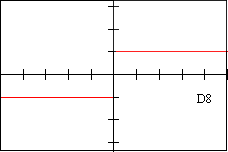
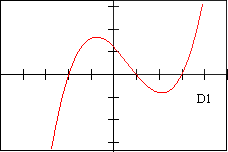
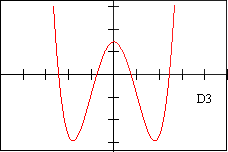
Page 4 - Derivative (or slope) Graphs, labeled D1-D12 [non-Calculus students may omit]
-
Page 5 - Derivative (or slope) Descriptions, labeled d1-d12[non-Calculus students may omit]
-
Key (to be given when scored)
Student name(s)______________________ How many minutes to complete Matching?______
[20 pts] Marching Chart
| Function Graph | Function Notation f(x) = |
Function Description | Function Values | Derivative Graph | Derivative Description |
| F 1 | E | f | V | D | d |
| F 2 | E | f | V | D | d |
| F 3 | E | f | V | D | d |
| F 4 | E | f | V | D | d |
| F 5 | E | f | V | D | d |
| F 6 | E | f | V | D | d |
| F 7 | E | f | V | D | d |
| F 8 | E | f | V | D | d |
| F 9 | E | f | V | D | d |
| F 10 | E | f | V | D | d |
| F 11 | E | f | V | D | d |
| F 12 | E | f | V | D | d |
Analysis Questions :
1. [5 pts] At the beginning of the matching, how did you start matching cards? (ex."I randomly picked a graph" or "I sorted the equations by roots")
2. [5 pts] How did your technique or approach change after you had matched about half of the equations & graphs?
3. [10 pts] While matching each equation to the corresponding graph, which technique(s) did you identify or use? Fill in the table below by:
- Write an "f" in the box if you used the function description with that technique
- Write an "E" in the box if you used the function notation with that technique
- Write a "V" in a box if you used the function values with that technique
- Write a "D"in a box if you used the graph of derivative with that technique
- Write a "d" in a box if you used the description of the derivative with that technique
- Put a “NA” for any technique you are not familiar with.
- Leave blank if you did not use the technique.
- You may put more than 1 answer in each box.
| Matching Technique | F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 |
F11 |
F12 |
| maximum or minimum points (extrema) | ||||||||||||
| zeroes, roots, or intercepts | ||||||||||||
| substitute values in for x to find f(x) or determining point values on graph |
||||||||||||
| I have the notation and graph memorized | ||||||||||||
| I have the function notation and the description memorized (example: x^2 is parabola or "U-shaped") |
||||||||||||
| translations (shifts up/down or right/left) | ||||||||||||
| coefficient values or dilation/compression | ||||||||||||
| symmetry (odd, even, neither) | ||||||||||||
| type of function (i.e. rational, polynomial of degree n, piecewise, etc.) | ||||||||||||
| inflection points | ||||||||||||
| guessing / process of elimination | ||||||||||||
| Other (explain below) |
Other techniques used:
4. [5 pts] Based on your checkmarks in the chart:
- What techniques are you good at? Why?)
- What techniques are you weakest at? Why? (note: time constraints
should not be considered
- What other patterns do you see in your matching process? How
do these patterns affect your understanding of the relationships
between derivatives and functions.
5. [5 pts] If you did this matching game over again, what would you do to make your matching:
- more accurate--if you missed any, explain, in detail, what
is the reason for the error(s)
|
|
0.5, -3 |
2.5, -1. |
|
V 4
-3.000, 0.545 |
V 5 |
V 6
-1.4, 1.4 |
|
V 7
-1.4, 0.5 |
V 8
|
V 9
-2., -4. |
|
V 10
1.0, -0.3 |
V 11
-5., -15. |
V 12
0.5, 0. |
|
E2 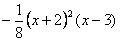 |
E3 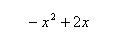 |
E10 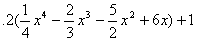 |
E4
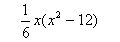 |
E5
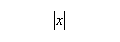 |
E9 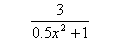 |
E6
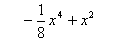 |
E12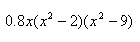 |
E8 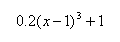 |
E1
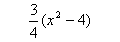 |
E11
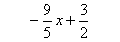 |
E7 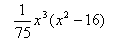 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
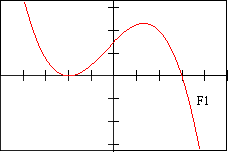
f 1 - DESCRIPTION OF FUNCTION The function has local maxima at x = -2 and x = 2
|
f5 - DESCRIPTION OF FUNCTION This is the graph of a linear function.
|
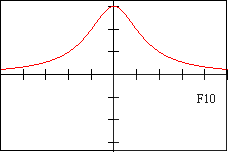
f10 - DESCRIPTION OF FUNCTION This function never decreases
|
f9 - DESCRIPTION OF FUNCTION This is the graph of a quadratic function with a negative leading coefficient
|
This even function is decreasing when x<0 and increasing when x>0
|
f6 - DESCRIPTION OF FUNCTION This function has critical poinst at x=-2, x=1, and x=3
|
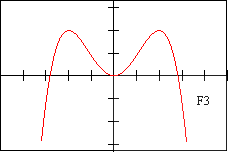
f3 - DESCRIPTION OF FUNCTION This odd function has a triple root at x=0, as well as roots at x=4 and x=-4
|
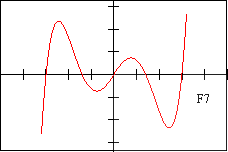
f7 - DESCRIPTION OF FUNCTION On this graph, x=-2 is both a root of the function and a critical point
|
f11 - DESCRIPTION OF FUNCTION This function has a point of inflection at x=0
|
f2 - DESCRIPTION OF FUNCTION This function has four critical points.
|
f4 - DESCRIPTION OF FUNCTION This is the graph of an absolute value function.
|
f8 - DESCRIPTION OF FUNCTION This function has a horizontal asymptote at y=0
|
 |
 |
 |
 |
 |
 |
 |
||
 |
 |
d 1 - DESCRIPTION OF DERIVATIVE The graph of this derivative is less than or equal to zero for all x in [-3,3]. The derivative graph is symmetric to the y-axis.
|
d5 - DESCRIPTION OF DERIVATIVE The graph of this derivative is a line that has a positive slope.
|
d9 - DESCRIPTION OF DERIVATIVE The equation of this derivative would have the general form
:
|
d2 - DESCRIPTION OF DERIVATIVE The graph of this derivative is positive is positive when x<0 and is negative when x>0
|
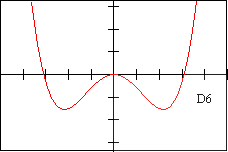
d6 - DESCRIPTION OF DERIVATIVE The slope of this graph is always -2
|
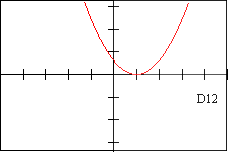
d10 - DESCRIPTION OF DERIVATIVE The graph of this derivative is an even function with a local maximum at x=0
|
d3 - DESCRIPTION OF DERIVATIVE The graph of this derivative isnegative and constant for all x
|
d7 - DESCRIPTION OF DERIVATIVE The derivative is positive when x<-2 and when 0<x<2 and is negative everywhere else.
|
d11 - DESCRIPTION OF DERIVATIVE The graph of this derivative is positive when | x | > 2
|
d4 - DESCRIPTION OF DERIVATIVE The graph of the derivative is a cubic polynomial with a positive leading coefficient
|
d8 - DESCRIPTION OF DERIVATIVE The derivative is always greater than or equal to zero.
|
d12 - DESCRIPTION OF DERIVATIVE The graph of this derivative is undefined when x=0, but is constant for x<0 and for x>0
|
| Function Graph | Function Notation f(x) = |
Function Description | Function Values | Derivative Graph | Derivative Description |
| F 1 | E 2 | f 7 | V 5 | D 4 | d 9 |
| F 2 | E 4 | f 11 | V 8 | D 7 | d 11 |
| F 3 | E 6 | f 1 | V 12 | D 11 | d 7 |
| F 4 | E 1 | f 12 | V 2 | D 9 | d 5 |
| F 5 | E 3 | f 9 | V 3 | D 2 | d 6 |
| F 6 | E 5 | f 4 | V 6 | D 8 | d 12 |
| F 7 | E 12 | f 2 | V 7 | D 3 | d 10 |
| F 8 | E 11 | f 5 | V 10 | D 10 | d 3 |
| F 9 | E 10 | f 6 | V 1 | D 1 | d 4 |
| F 10 | E 9 | f 8 | V 4 | D 5 | d 2 |
| F 11 | E 8 | f 10 | V 9 | D 12 | d 8 |
| F 12 | E 7 | f 3 | V 11 | D 6 | d 1 |
TOTAL POINTS for a QUIZ Score: 50 pts
- Matching Chart Above: 20 pts (5 points per column, -1 for each TWO missed matches in a column):
- Question #1: 5 pts
- Question #2: 5 pts
- Question #3 (chart): 10 pts
- Question #4: 5 pts
- Question #5: 5 pts
